x264 码控-Prerequisites
RDO理论
根据RDO理论:
$J=D+\lambda\cdot R$
其中:
- J表示最终的衡量数据,也被称为RD cost(rate-distortion cost)
- D表示失真的衡量数据
- $\lambda$表示拉格朗日乘数
- R表示数据量的衡量数据
拉格朗日乘数法,在数学中的最优化问题中,是一种寻找多元函数在其变量受到一个或多个条件的约束时的局部极值的方法。这种方法可以将一个有n个变量与k个约束条件的最优化问题转换为一个解有n + k个变量的方程组的解的问题。这种方法中引入了一个或一组新的未知数lambda,即拉格朗日乘数。
RQ模型
QP参数会用于量化模块,它会引起视频图像的失真,它也直接决定着残差数据的大小,即很大程度影响最终编码后码流的大小。既然QP既要影响图像失真,又会影响码流大小,而选择最佳QP又是个优化过程,这其实就是视频编码里面的率失真优化RDO理论。
码率控制过程涉及到RDO,那x264的R-D模型是什么呢?
$bits=coeff\times\frac{SATD}{qscale} + offset$
其中:
- bits表示编码当前帧需要的bits
- SATD表示当前帧复杂度
- coeff表示历史数据的影响系数
- offset表示历史数据的影响程度
- qscale实际上表示的就是拉格朗日乘数
从上面的公式可以看出:复杂度不变,bits和qscale成反比;qscale不变,bits和复杂度成正比。
那么qscale和qp是怎么联系的呢?
$QP=6\times\log_{2}(\frac{qscale}{0.85})+12$
可以看出qscale越大,qp越大,反之亦然。
VBV
VBV解决的问题?
假如编码是面向存储的,编码出来的码率随便怎么波动都无所谓,只存在本地就OK。
但是如果编码是面向传输的,就要考虑到网络的带宽问题,以及网络的抖动,如果编码出来的码率变化非常大,那么很不利于传输,比如为了帧的质量,突然编出来一个很大的帧,需要传输很久,那么解码端那边就会需要等很久,体现在播放时长时间卡住。
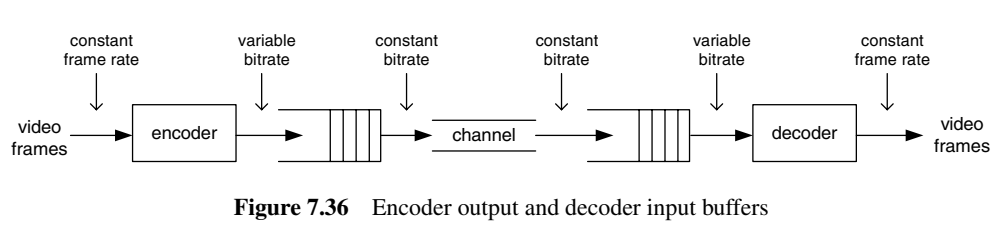
因此需要一个buffer来平滑码率,处理每帧编码后大小不一(变化的码率)和恒定的输出码率的矛盾。
什么是VBV?
VBV全称Video Buffer Verifier(视频缓冲区校验器),其实是一个leaky bucket漏桶模型。编码端和解码端都有这样的一个buffer,编码端的buffer是用来模拟解码的过程,从而有效得控制好码率。VBV可以理解为一个水池,水池存在有限的容量大小,且有一个注水口和一个出水口, 每编码一帧后都会往水池里面注入一部分水,同时也会流出一部分水。
- 注入的速率是变化的,每编码完成一帧会注入,注入的大小是实际的编码bits
- 流出的速率是固定的,每编码完成一帧会流出,流出的大小是期望的编码bits
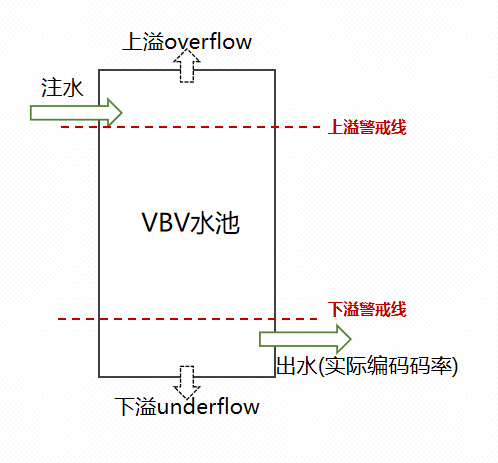
这就表示:
- 如果实际编码码率低于目标码率,那么水池的水会持续上涨,直至超过上溢警戒线(overflow)
- 如果实际编码码率高于目标码率,那么水池的水会持续下降,直至低于下溢警戒线(underflow)
X264中的VBV
几个重要的vbv变量:
- vbv_buffer_size: VBV buffer的容量(bits)
- vbv_max_rate: 每秒从VBV buffer中流出的速率(bps)
- buffer_rate:frame从VBV buffer中流出的bits,等于frame的duration * vbv_max_rate
- buffer_fill:当前VBV buffer实际被填充的大小(bits)
- vbv_buffer_init: 系数,用来控制初始的buffer_fill_final
- buffer_fill_final: 一帧编码实际完成后,VBV buffer实际被填充的大小(bits) ,初始值等于vbv_buffer_size * vbv_buffer_init